Volumes by Integration

Volumes by Integration: Disk Method

It would look something like this:

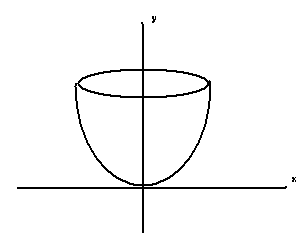
Now, imagine a very thin disk, as shown below. This disk can cover the entire volume by sweeping from bottom to top, changing its diameter as it moves.

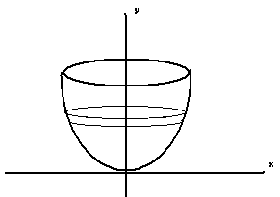
The thickness of the disk is dy. 

The volume of the differential disk is:

dV=pr²dy

Where in this case the thickness of the disk is dy and the radius is x.

        So:     dV=px²dy

Before we can integrate this, it needs to be in terms of y (since we have the dy. If we had dx, everything would need to be in terms of x.)

So, if y=x², then x=y^1/2. We can plug this in for x:

              dV=p(y^1/2)2dy = pydy.

This is easy to integrate.

           

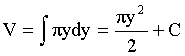
Let’s look at another example using dx this time.