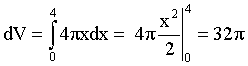Volumes by Integration

Volumes by Integration: Disk Method

Now sketch a differential element, a volume disk, with thickness dx.

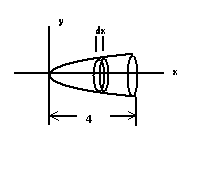
OK. Let’s write the equation for the volume of the disk, dV:

        dV=pr²dx

Now we have to get the whole equation in terms of x. Note that the radius of the disk, r = y. And y = 2x^1/2. Let’s plug this into the equation for dV.

   dV=p(2x^1/2)²dx = p4xdx

Now we can integrate. This time, we’ll include limits. Note that the disk would sweep along the x axis from 0 to 4.

Procedure