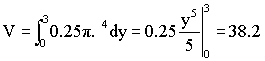Volume by Integration: Disk Method Practice Problem Solution
1. Rotate the area bounded by x=0, y=0, y=3, and x=0.5y2 about the y axis and determine the volume.
Here is the area:
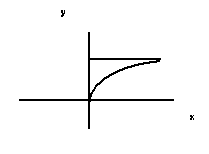
When we rotate this about the y axis we get this volume:
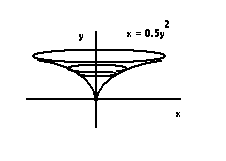
The disk element has been drawn in. Now we write an equation for the volume of the disk:
dV= pr2dy
The radius of the disk is x in this case. But we need everything in terms of y since we have dy. So we use the equation for y in terms of x and plug that in.
dV= p(0.5y2)2dy = 0.25py4dy
We can integrate this. First let’s choose limits. The disk would move along the y axis from 0 to 3. Then: