Hyperbola
In a hyperbola, the difference between the distances from two fixed points is constant. These fixed points are the foci of the hyperbola. These points are located at (c,0) and (-c,0).
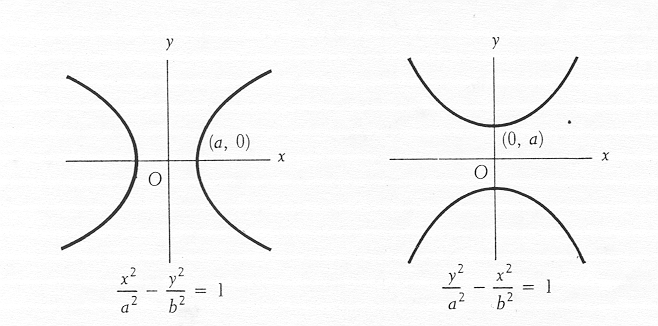
The standard form is: x2/a2 – y2/b2 = 1
Also: a2 + b2 = c2
Note that this looks just like the ellipse equation except for the minus sign.
To sketch a hyperbola, you should first sketch its asymptotes. The asymptotes are seen below.
$$$$
EXAMPLE: Sketch x2 – 4y2 – 16 = 0
Solution: First rearrange this to look like the standard form. How?
Add 16 to both sides. Then divide by 16. You get:
x2/16 – y2/4 = 1
So a = 4 and b = 2. Now connect the points (4,2), (-4,-2) and (4,-2), (-4,2). These two lines are the asymptotes.
Calculate c: c2 = a2 + b2 = 42 + 22
c = 4.472
So the foci are (4.472, 0) and (-4.472, 0).
Now we can sketch the hyperbola.
$$$$
Click here for practice problems.





