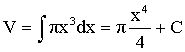Volumes by Integration: Shell Method
This is a second method for determining the volume created by revolving an area about an axis. Sometimes the disk method won’t work, so we need another method.
Let’s look at the volume below. What if we want to determine the volume of the shaded area outside the "nose cone" shape? A disk won’t fit. Instead of sweeping a disk through the volume, we use a "shell".
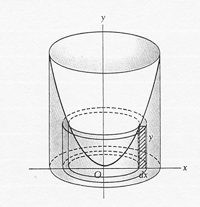
Imagine a shell to be a very thin cylinder, of thickness dx, in this case, or dy. For the sketch above, the height is y and the radius is x.
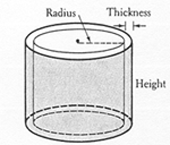
So we can write the equation for the volume of the shell, dV=circumference * height * thickness:
dV=2pr h dx or dV=2pxy dx
Before we can integrate, the equation needs to be all in terms of x, so we need the equation for y in terms of x. Say y=x2. Then:
dV=2px3 dx
Integrating: