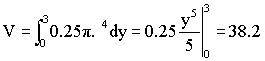Volume by Integration

Volume by Integration: Disk Method Practice Problem Solution

    1. Rotate the area bounded by x=0, y=0, y=3, and x=0.5y² about     the y axis and determine the volume.

   Here is the area:

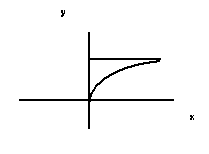
When we rotate this about the y axis we get this volume:

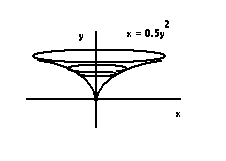
The disk element has been drawn in. Now we write an equation for the volume of the disk:

               dV= pr²dy

The radius of the disk is x in this case. But we need everything in terms of y since we have dy. So we use the equation for y in terms of x and plug that in.

                dV= p(0.5y²)²dy = 0.25py⁴dy

We can integrate this. First let’s choose limits. The disk would move along the y axis from 0 to 3. Then:

               

   Back to practice problems.