Applications of Derivatives
Graphing
We can get a better understanding of derivatives by studying the graph of equations and their derivatives.
Say we were given a graph of position and we wanted to determine the velocity and acceleration from that graph.
NEED SKETCH 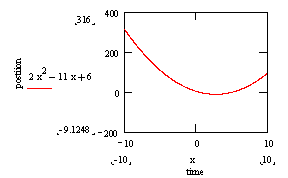
We know that the velocity, v = ds/dt. In other words, the velocity is the slope of the s-t graph. What is the slope (the tangent line) doing in the graph above?
It starts out negative and approaches zero, reaching zero slope at about t = 3. Then it becomes positive and steadily increases. So the plot of velocity versus time would look like this:
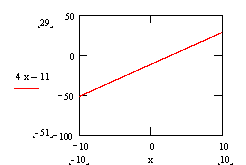
Then if we want the plot of acceleration versus time, we look at the slope of the v-t curve. The slope of this curve is positive and constant, so the a-t curve looks like this:
NEED SKETCH





