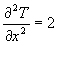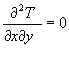Example: Location of a Local Minimum, Maximum or Saddle Point
A flat plate is heated such that the temperature, T at any point (x, y) can be described as T = x2 + 2y2 – x. Find the temperature at the coldest point on the plate.
Solution
Take the partial derivatives and set them equal to zero:
x = 1/2
y = 0
Now plug these values back into the equation for temperature:
T(0.5, 0) = (0.5)2 + 2(0)2 – 0.5 = -0.25C
But is this a minimum (coldest temperature)? Calculate D to check. Find find the second partial derivatives.
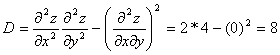
Then since D>0 and 
>0, it is a minimum point.
Practice Problems
