Calculating the voltage across a capacitor.
The voltage, V, across a capacitor can be expressed as:
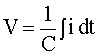
A 1.25F capacitor that has an initial voltage of 25.o V is charged with a current that varies with time as i = t (t2 + 6.83)1/2. Find the voltage across the capacitor at 1.00seconds.
Write the initial equation.
![]()
Now do the substitution for u, du, n.
u = t2 + 6.83 du = 2t dt n = 1/2
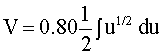
Now integrate:
V = .8* 2/3u2/3 +C = 0.267(t2 + 6.83)3/2+ C
To solve for the constant, C, we need a set of initial conditions.
When t = 0, V = 25V.
So, 25 = 0.267((0)2 + 6.83)3/2+ C
C = 20.2 V
Then V = 0.267(t2 + 6.83)2/3+ 20.2.
And when t = 1 sec, V = 26.0V





