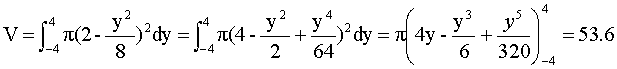Volume by Integration

Volume by Integration: Disk Method Practice Problem Solution  

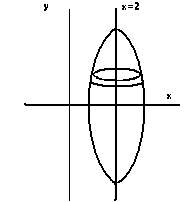
    3. Find the volume of y² = 8x rotated about the x = 2 axis.

Now write the equation for the volume of the disk, dV= pr²dy.

The radius, r is not x. Looking at the sketch we see that r=2-x. So:

        dV= p(2-x)²dy = p(2-y²/8)²dy

Now set up the integral. The limits are in the y direction at the end point of the object where x=2. Solving for y at x=2, we get +4 and -4.