Using Integration to find the Area between 2 Curves
What if you want to determine the area between two curves, y2and y1 , like the area shaded below?
We use the same approach: sketch the differential area dA, then write the equation:
dA = (y2-y1) dx
Where y2 is the top curve and y1 is the bottom curve.
Note : Sometimes using dA = (y2-y1) dx won’t work, but dA = (x21 – x1) dy will.
Then you need to find out where the two curves intersect. Set the 2 equations equal and solve for the x. You should get two solutions. These are the limits of integration.
Example: Find the area between y2= 2x – x2 and y1= x4.
NEED SKETCH
dA = (y2-y1) dx = ((2x – x2 )- x4) dx
Solve for the limits:
2x – x2 = x4
x4+ x2 – 2x = 0
x(x3+ x – 2) = 0
x = 0, 1 So:
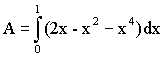
A = x2 – x3/3 – x5/5 between 0 and 1
A = 7/15





